Angle de déformation SOLIDWORKS Simulation

Comment calculer l’angle de déformation lors de la sollicitation d’un composant dans SOLIDWORKS Simulation ?

 

Lors de l’exploitation des résultats d’une étude de SOLIDWORKS Simulation, il est possible d’obtenir automatiquement les déplacements des différents nœuds du composant étudié. Ces valeurs de déplacement peuvent être données pour un déplacement résultant, un déplacement directionnel orthonormé, ou même dans un repère cylindrique. Mais dans certains cas, ces valeurs de déplacement ne sont pas suffisantes, il peut être intéressant de connaitre le déplacement angulaire d’un nœud, ou l’angle de déformation SOLIDWORKS Simulation. Vous retrouverez ci-dessous les étapes nécessaires pour l’obtenir.

1. angle de déformation solidworks simulation : Définition de l’étude d’exemple

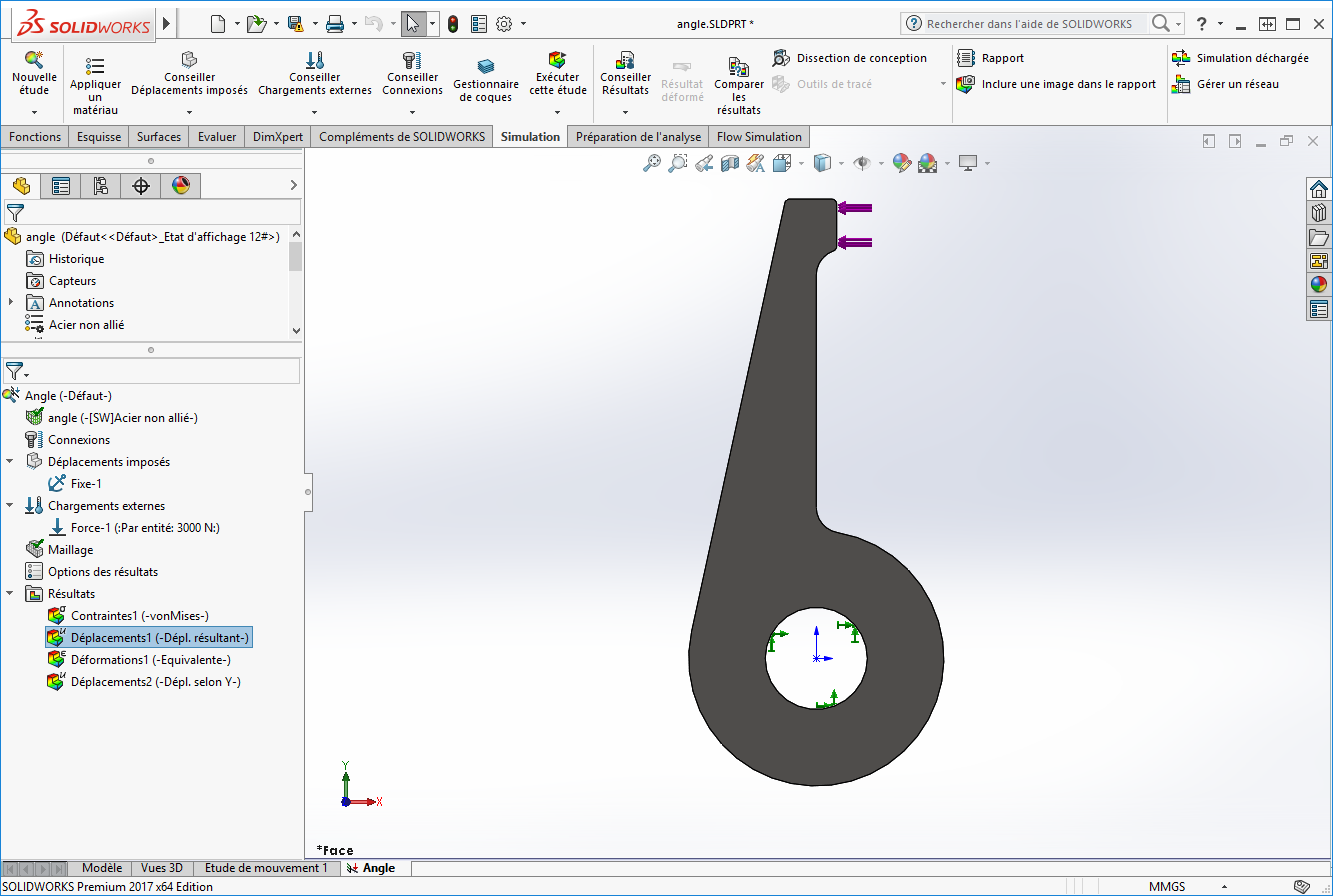
Tout d’abord, précisons que notre exemple est une pièce basique bloquée sur son axe. Elle est sollicitée par une force de 3000 N sur une face déportée, comme le montre l’image ci-dessous :

2. ANGLE DE DÉFORMATION SOLIDWORKS SIMULATION : Consultation des résultats

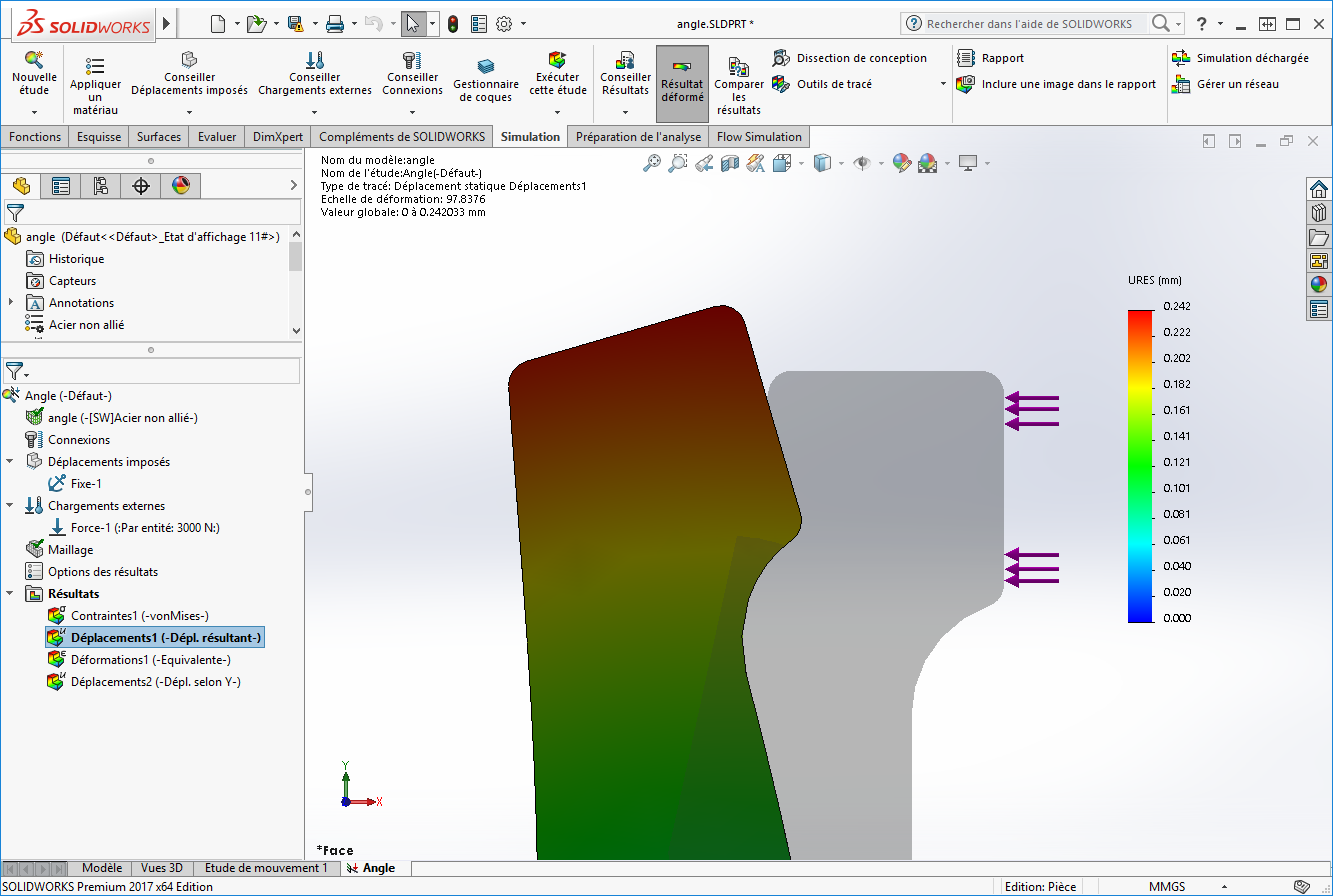
Les résultats de déplacement résultant sont de 0.242mm.

3. ANGLE DE DÉFORMATION SOLIDWORKS SIMULATION : Tracé de déplacement dans un repère cylindrique

Afin de pouvoir calculer l’angle de déplacement, nous avons besoin de récupérer les valeurs de déplacement dans un repère cylindrique. C’est pourquoi nous devons créer une entité axe dans SOLIDWORKS (géométrie de référence). Puis, nous devons créer un tracé de déplacement avec ces paramètres :

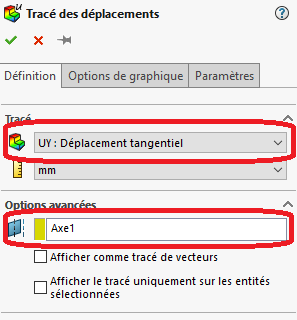
Ainsi, nous obtenons le déplacement tangent de chaque point dans le repère cylindrique de l’axe.

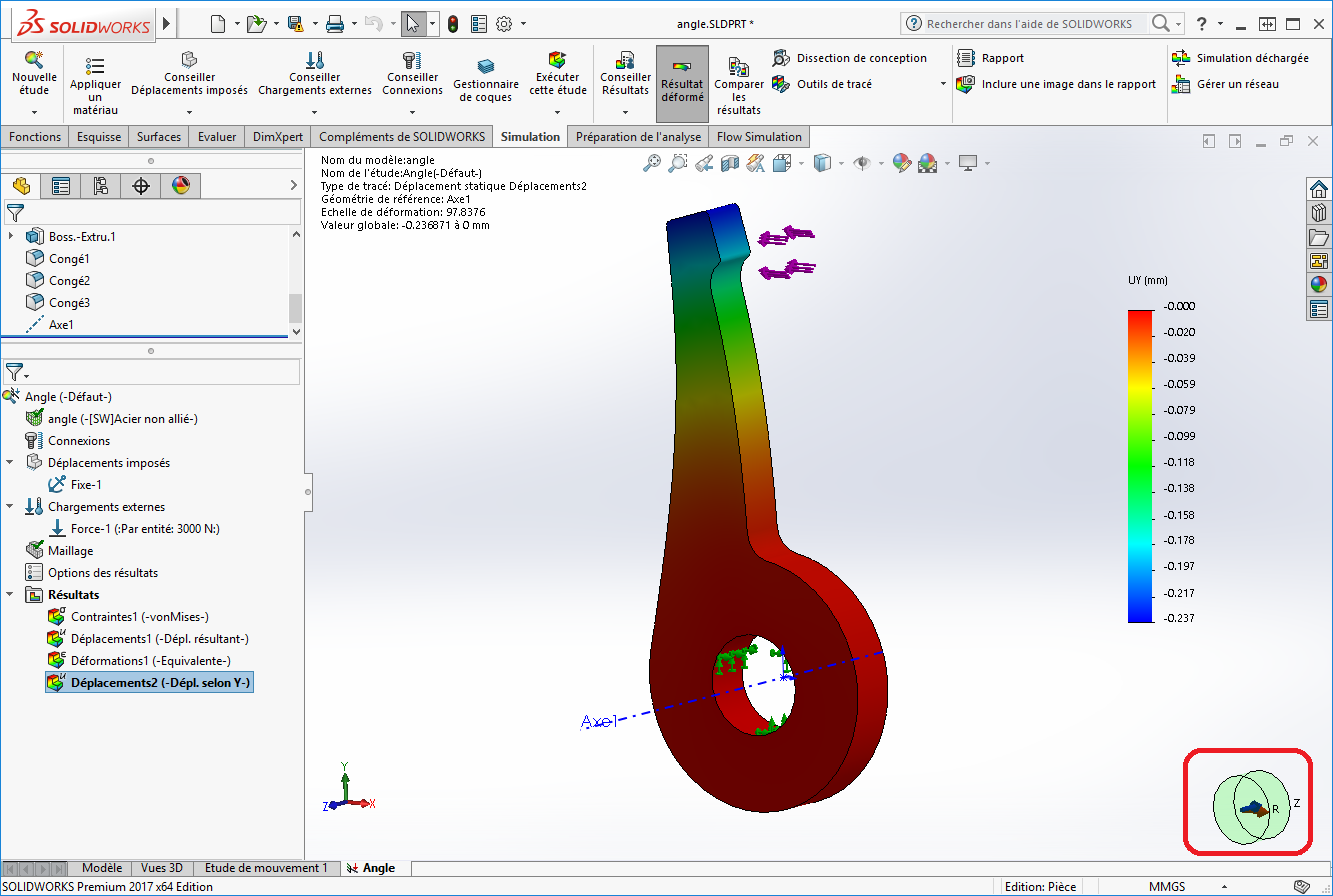
De plus, le cylindre en bas à droite du tracé indique que nous somme bien dans un repère cylindrique.

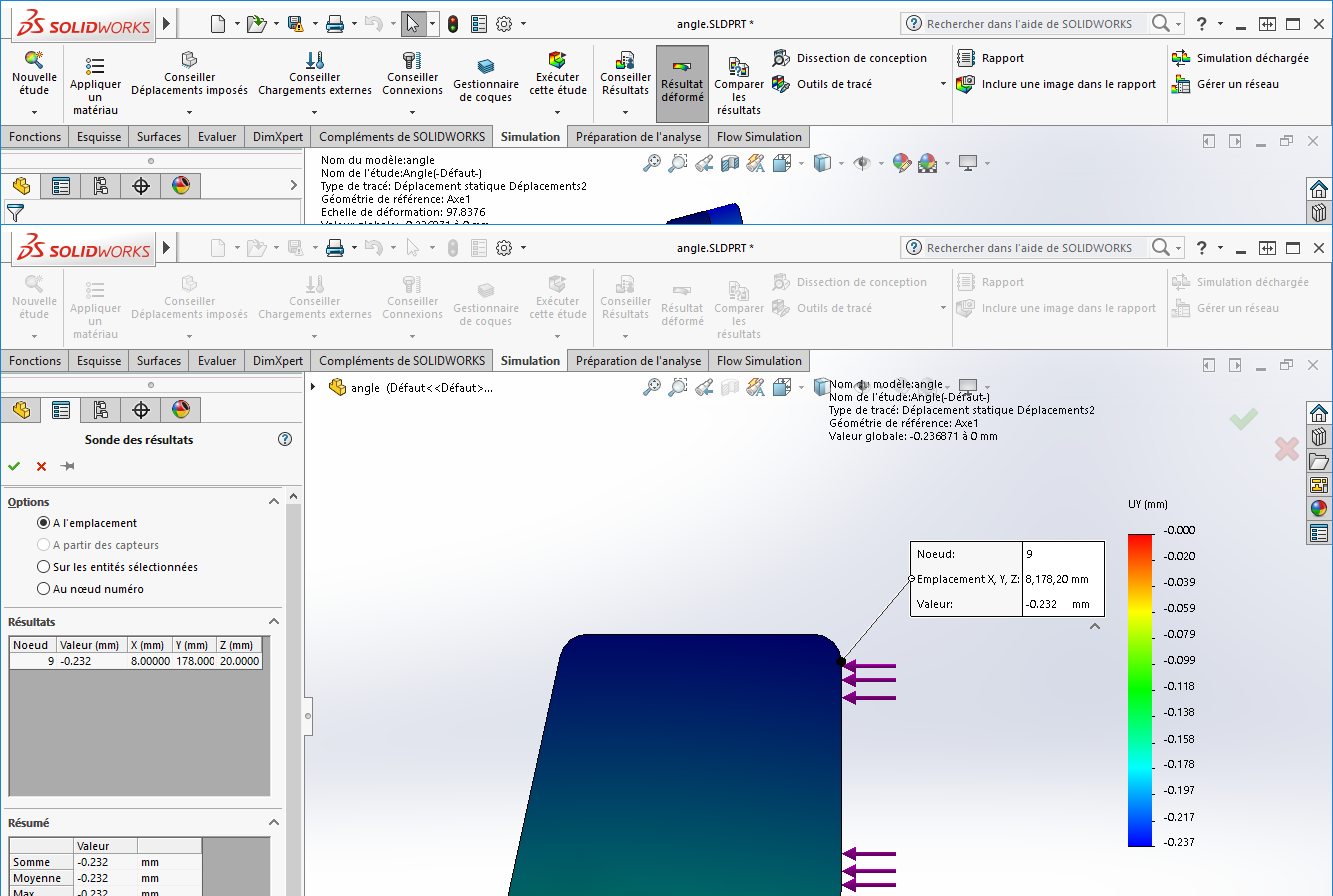
4. ANGLE DE DÉFORMATION SOLIDWORKS SIMULATION : Sonder les valeurs de déplacement tangentiel

Ensuite, la valeur que nous sondons dans ce tracé correspond au déplacement qu’effectue le point (nœud) le long de l’arc dont le centre est l’axe 1. (Longueur d’arc)

5. ANGLE DE DÉFORMATION SOLIDWORKS SIMULATION : calculer l’angle de déplacement

Pour connaitre l’angle θ en degré il suffit de résoudre cette équation : θ = (180×Lc)/(π×r) avec :    θ  : Angle Teta r  : Rayon Lc  : Longueur d’arc 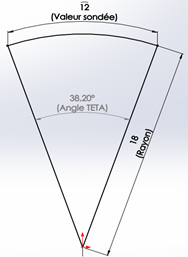Puis, pour une mise en pratique sur notre modèle, il faut s’appuyer sur les valeurs données par l’outil sonde : La valeur correspond à notre longueur d’arc, mais il nous reste à déterminer le rayon. Les valeurs de position du nœud vont nous servir à déterminer le rayon. Seules les positions en X et Y nous intéressent dans notre cas (problème plan et calcul d’angle dans le plan de Face). Attention, ces valeurs sont données à l’origine du composant SOLIDWORKS. Il peut être nécessaire de faire un changement de repère pour connaitre les valeurs au niveau de notre axe. Pour déterminer le rayon, nous allons utiliser le théorème de Pythagore : r = √(EX²+EY²) Avec :   r  : Rayon EX   : Position du point en X (éventuellement corriger du décalage de l’axe par rapport à l’origine de SOLIDWORKS) EY   : Position du point en Y (éventuellement corriger du décalage de l’axe par rapport à l’origine de SOLIDWORKS) Ainsi, nous pouvons calculer l’angle de déplacement de notre exemple : θ=(180×Lc)/(π×√(EX²+EY²)) θ=(180×0.232)/(π×√(8²+178²)) θ=0.0746°